6th Grade Math!
We ended the last week disucssing an introduction to statistics. Here is a good video from Khan Academy on this topic:
https://www.khanacademy.org/math/ap-statistics/summarizing-quantitative-data-ap/measuring-center-quantitative/v/statistics-intro-mean-median-and-mode
It’s a straight foreward look at the concept. We took notes for two days on this so you should be looking at your notes as you watch the video. Pause the video and look at your notes as you watch it to make sure you understand both the notes and the video. You can always email me if you have questions.
Okay, here is your problem of the week: Find the Mean, Median and Mode of the following data set:
60, 66, 73, 48, 29, 88, 81, 90, 99, 22, 114, 57, 56, 55, 12.
Remember for the median you’ll have to arrange the data points from smallest to greatest and find the number in the middle. You can use a calculator for this problem. When you’re done take a picture of your work and email it to me at the school email.
Good luck!!!
April 16th to April 23rd.
Okay, answers to last week’s work:
MEAN: Add up the numbers then divide by 15, the number of data points!
Sum: 896. Now divide by 15 to get….59.7333.
MEDIAN: Arrange the numbers from smallest to biggest then find the number in the middle!
The number in the middle is 60!
MODE: The most frequent number. Since no number repeats, occurs more than once, there is no mode.
New Stuff….
Stem and Lear plots! This is neat stuff. We take a data set like we did last week and display the data in this manner:
Data set: 5, 12, 18, 19, 29, 30, 31, 31, 31, 36, 40, 55.
Now the “tens place” make up the “stems” and the numbers in the ones place make up the “leafs”.
Stem [ Leaf
0 [ 5
1 [ 2 8 9
2 [ 9
3 [ 0 1 1 1 6
4 [ 0
5 [ 5
So watch the video then creat a stem-leaf plot of the following data set. Take a picture and send it to me.
22, 24, 38, 39, 41, 41, 41, 45, 45, 48, 48, 48, 59, 61, 61, 72
Have a great week!
April 27th to May 1st, 2020.
Last week we looked at the Stem-leaf plot for a set of data. Now we’ll learn about the “Pie Chart” The Pie Chart is predicated (based) upon percents. For example, let’s say I run a business and want to know where our water usage is going. I find out the percent of each type of use and I can present it in the following chart:

As you can see, the usage is clearly displayed. It is an effective means of giving information to an audience and it more efficient than just listing out the percent numbers all by themselves. Governments, businesses and even households (Microsoft Money will display your spending in a pie-chart if you want) use these type of charts all the time so you should know and be comfortable with them.
So how do we make them? We just multiply the percent each data catagory (Toilet water, leaks, shower water) by 360. Why 360 do you ask? Because a circle is made up of 360 degrees!
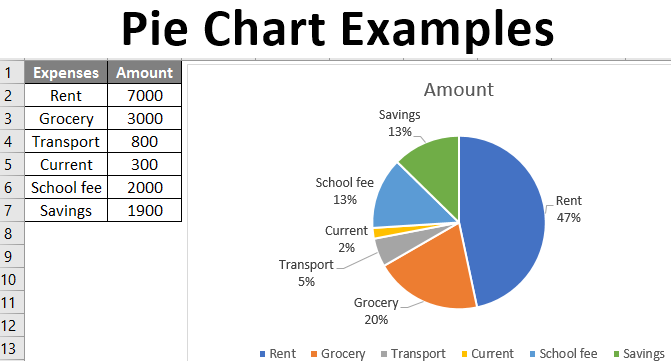
This is from a peron’s account using Microsoft Money. As you can see, they spend most of their money on rent. So
let’s see how they got it. Okay, they added all the spending amounts together and got $15000. Now to find out how many degrees make up RENT we take the amount of rent, $7000, and divide this by the total income, $15000….=.47 (which is 47%). Now we take .47 and multiply it by 360 degrees and we get 196.2 degrees. So do you see how the “RENT” in the pie chart makes up just a little less than half the circle (in blue).
Now look at the category called,”Current” (that is how much money they have on hand in their purse or wallet). We take the $300 in CURRENT and divide it by $15000 and get .02 (2%). I now multiply .02 by 360 and get 7.2 degrees, which as you can see in the pie chart is a very tiny slice of the pie!
Homework:
You are to take the data from the following table and make a pie chart out of it.
Mr. Lowden Russell has 100 students broken down in the following catagories:
11 year-olds: 2
12 year-olds: 44
13 year-olds: 40
14 year-olds: 10
15 year-olds: 4
Make a pie-chart displaying the data in a manner similar to the Microsoft Money chart! Take a picture, showing clearly the percents on the pie-chart, and email it to me.
Have a great weak!
Week of May 4th to May 7th.
Probability.
We only briefly touched on this subect before school closed early. It is important and you will go into greater detail in your 7th grade. Let’s go over what I would have liked to have done last April…
Let’s define some important words:
Probability: The likelihood of an “event” happening, or not happeing. Usually expressed as a percentage (the chance of rain on Friday is 2%) or a fraction (The chance of drawing an Ace from a deck of cards is 4/52)
Sample Space: The total number of possible outcomes. Example, when you roll a single six-sided die in a board game there are 6 outcomes (1 through 6). So your sample space is 1,2,3,4,5,6. Or if you’re playing with a deck of cards there are 52 different cards so your sample space is the list of 52 differnt cards-I won’t list them all, but it would go like this...2 of Diamonds, 2 of hearts, 2 of clubs...and so on. The Sample Space is important to know as that is your denominator!!!
Desired Event: What your looking for. For example, I want to find the probability of rolling a prime-number on a single die. I would first have to identify which numbers from one to six are prime! 1, 2 , 3 and 5 are prime numbers.
Concept:
Probability calculation: Desired event (total) divided by total sample space. Easy! Again, it will be expressed as a fraction or a percent.
Examples: What is the probability of rolling a prime number on a single six-sided die?
Well, you need the number of prime numbers, which I listed above as 1,2,3,5. So there are 4 desired events. Now I divide this by the total numbe in the sample space: 1,2,3,4,5,6.
P(rollling a prime number)= 4 divided by 6. 4/6= 2/3 = 67% (rounded).
Another example: What is the probability of picking an Ace or a King from a standard deck of cards?
Okay, we know our sample space, the denominator in our calculation is 52 since there are 52 cards in a standard deck of cards. So our numerator is the number of Aces plus the number of Kings! 4 Aces and 4 Kings are in a standard deck of cards. So our numerator is 4+4=8.
P(drawing an Ace or King) = 8/52 = 2/13 or 15.3%.
Problems for this week to be turned in:
1. What is the probability of drawing an Ace, King or Queen from a standard deck of cards?
2. What is the probability of rolling a 1 or 3 on a single six-sided die?
3. What is the probability of rollling an odd number on a single six-sided die?
4. What is the probabiity of rolling an even number on a single six-sided die?
5. What did you notice about the answer to #3 and #4?
6. There are 13 students in Mr. Russell’s 5th period class. If each student places their name on a slip of paper in a hat and Mr. Russell draws a single slip of paper, what is the probabilty that Mr. Choses either Shane or Anshanti’s name out of the hat. Remember, you have to identify the numerator and denominator.
7. On a shelf in Mr. Russell’s class there are 4 math books, 2 science books, 8 history books and 9 English lit books. What is the probability that Mr. Russell will randomly select a history book? Write your answer as a fraction.
8. Using the same sample space in problem #7 above, what is the probability of Mr. Russell picking a math book or a science book from the shelf?
9. Mr. Russell found a 10-sided die to use in an experiment. What is the probability of Mr. Russell rolling a prime-number on that die?
10. Lowden, Mr. Russell’s brother, said he would pick either Saturday or Friday of next week to go to Socorro. What is the probability He chooses Friday to go to Socorro.
Next week we’ll go into greater detail on this subject. Have a great week!
Compound Probabilities May 11th to May 14th
Last week we worked on simple probability computations. This week we get a little more challenging.
Example 1: What is the probability of rain in two successive days if the probability of each day there being rain is 30%?
Answer: Just multiply! We know 30% written as a decimal is .3. Since we are looking at two days in a row, each day having a 30% chance of rain, we just multiply .3 x .3 = .09. So, converting .09 back to a percent (moving the decimal two places to the right) we get 9%!
Example 2: Now let’s say they ask,”What is the probabiity of rain on the first day and not-rain on the second day using the same 30% chance either day?”
Answer 2: Well if there is a 30% chance of rain that must mean we have a 70% chance of no rain! All possible outcomes must add up to 100% in probability. So two find the probability of the first day being rain and the second day there being no rain we multiply 30% x 70% = .3 x .7 = .21 = 21%.
Example 3: If we roll a six-sided die three times what is the probability that we roll a “2” three times in a row?
Answer 3: We can also use fractions instead of decimals to find probility. The chance of rolling a “2” on a six-sided die is 1/6. So to roll that three times in a row is Is 1/6 x 1/6 x 1/6 = (1x1x1)/(6x6x6) = 1/216. If you divide one by 216 you get .004629 or .4629%, that is less than a one-percent chance of it happening.
Here is a good video you can watch:
https://youtu.be/yUaI0JriZtY
Example 4: Let’s say there are 5 red marbles, 2 blue marbles and 8 green marbles in a bag. What is the probability of picking a red marble, putting that marble back in the bag, then picking a blue marble?
Answer 4: What is the probability of pickinga red marble? 5 reds out of a total of 15 marbles (the total number of marbles in the bag). So 5/15. What is the probability of picking a blue marble? 2/15. Now we multiply: 5/15 x 2/15 = (5x2)/(15x15) = 10/225! you can leave your answer as a fraction.
Home work :
1. What is the probability of rolling a prime number two times in a row on a six-sided die?
2. On a ten-sided die, what is the probability of rolling a “8” then a “7” on two rolls of the die?
3. If you flip a coin 4 times, what is the probability of a “heads” coming up all four times?
4. What is the probability of flipping a coin and getting a “tails” then rolling a six-sided die and getting a “4”? Just multiply each probability.
5. If there is a 50% chance of flipping a coin and getting a tails, what is the probability of getting a heads? Why?
- If there is a 20% chance of rain on Friday and Saturday, what is the probability of it raining on both days?
- Using the same percentage chance from #6, what is the probability of rain on Friday and NO rain on Saturday?
- Using the same percentages in #6, what is the probability of no rain on both days?
Good luck! Make sure you show your work and email me your answers!

 Additional settings for Safari Browser.
Additional settings for Safari Browser.



