Week May 4th to May 7th : SLOPE
We’ll spend a great deal of time next year on calculating the slope of a line, equation of a line from two points, y-intercept, x-intercept. Of course, we’ll also look at the real-world applications of lines, but we’ll start with slope calcuation.
First, let us remember we did do basic slope calculations in December. Let us define slope, again:
SLOPE = Rise/Run= Change in Y over change in X. See the graphic below:
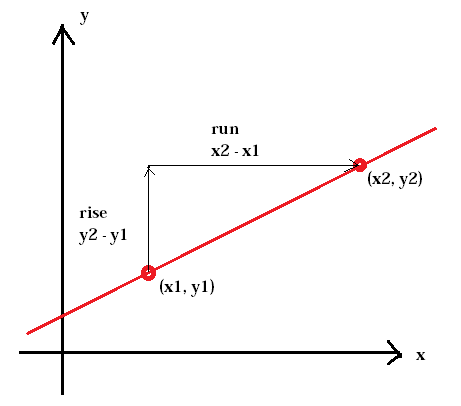
The Rise is the difference (subtraction) between the y-coordinates of two points. The Run is the difference between the x-coordinates. After doing those two subtractions you then divide to obtain the slope. Usually we prefer to leave the slope in fraction form, although it can be expressed as a decimal. You don’t have to graph the two points to do the calculation of the slope, but you should be comfortable calculating the slope from two points on a graph.
Example: Calculate the slope of the line connecting the points (2,5) and (7,9).
Okay, you should first determine which point will be X1, Y1. It doesnt matter. Let me repeate:: it doesn’t matter.
Let’s say the first point is X1,Y1, so X1 = 2 and Y1 = 5. Thus X2 = 7 and Y2 = 9
So the Rise divided by the Run is (Y2-Y1) divided by (X2 – X1)….This will be the slope.
Slope = (9 – 5) divided by (7 – 2) = 5 divided by 5 or just 1. The slope is 1 or 1/1. Notice, wrote “1” as a fraction: 1/1.
Slopes can be positive, negative, zero (which is a horizontal line) or “undefined” (a vertical line). Let’s look at an example of a line with negative slope…

Let’s say point 1 is (3,3) and therefore point 2 is (0,6). So we calculate the slope as we did in the first example:
Slope = (Y2 – Y1)/(X2 – X1) = (6 – 3)/(0 – 3)= 3/-3 = -1/1. Notice, as the line moved to the right, the line fell, went lower and lower. That is what it means to have a negative slope.
Here is another example, this time with positive slope (notice it is rising as we move to the right):

Okay, like I said previously, it doesn’t matter which point is Point 1 (x1,y1). Let’s say point B(15,5) is point 1, therefore point 2 is A(30,25). Let’s find the slope:
Slope = (y2-y1)/(x2-x1) = (25 – 5)/(30-15) = 20/15! We can reduce this fraction by dividing out the common factor of 5 from both numerator and denominator, 20/15 = 4/3. That means for every 3 units we go to the right we go up 4 units.
Real-world example:
Ms Jenna-Korbaski worked 4 hours and earned 20 dollars. She then worked the next day 8 hours and earned 40 dollars. What is her “rate” of pay per hour (the slope)?
Solution: Let’s first write the information as coordinate points with x being hours worked and y being money earned.
Point A: (4,20)
Point B: (8,40).
Nice, let’s find the rise/run, or the slope:
(Y2 – Y1)/(X2-X1) = (40 – 20)/(8 – 4) = 20/4= 5/1. Notice, I could have written this as a simple “5” since 5 divided by 1 is 5, but we like to leave it in fraction form. The real-world interpretation of what this slope tells us is for every 1 hour Jenna earns $5.
Example of Zero slope:
Take point A to be (-3,9) and point B to be (12,9). Calculate the slope:
Slope = (Y2 – Y1)/(X2 – X1) = (9-9)/(12- -3) = 0/15 (notice that X1 was a NEGATIVE 3 so 12 minus a negative 3 is the same as a 12 PLUS 3). So what is 0 divided by 15? ZERO. Zero divided by any number, other than zero, is ZERO. That means the line is horizontal. As you move to the right along the line it doesn’t go up or down.
Example of an Undefined Slope:
Take point A to be (7,62) and point B to be (7,6). Calculate the slope:
Slope = (Y2 – Y1)/(X2 – X1) = (62 – 6)/(7 – 7)= 56/0. Guess what? You can’t divide by zero! If you type into the calculator 56 divided by zero you get ERROR. That means anytime you have a zero in the denomiinator of a slope calculation the slope is undefined!!!!
Now, in case you need a different perspective on how to calculate slope here is a Khan Academy video:
https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:linear-equations-graphs/x2f8bb11595b61c86:slope/v/slope-of-a-line
Homework:
Calculate the slope of the follwoing lines with the two given points (Leave answers as fractions and show your work)
- A(2,8) B(8,5)
- X(-3,-5) Y(4,6) [Make sure you are careful with the negative numbers.]
- M(0,8) N(-8,9)
- A(4,5) B(4,10)
- X(8,12) Y(100, 12).
Calculate the slope from any two points on the graph. Just use two points:
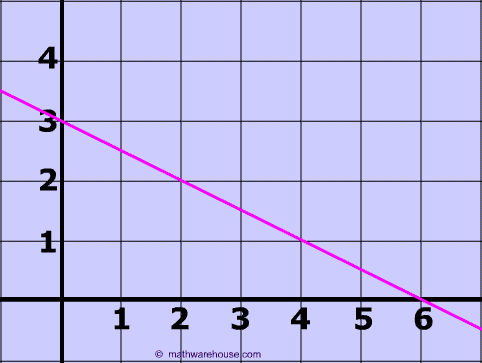
Real-world problem:
Mr. Anasazi is a plumber. If he works for 3 hours fixing the plumbing he makes $180. If he works for 5 hours he will make $260. What is Mr. Anasazi’s hourly rate (Just write two points from the above information and calculate the slope in Dollars/hours.).
Good luck! Make sure you show all your work and send the information to me with pictures!
Week of May 11th to May 14th: More on Slopes/Lines.
So why do we learn about slopes (also known as “rates”)? Because we can construct equations of lines using slopes and points!
The equation of a line, in what is called, “Slope-intercept” form is:
Y = mX +b.
m, as we saw last week, is the slope, and as we know we do two subtractions followed by a single division. You did last week’s homework, yes?
Now, the lower case “b” is called the “Y-intercept”. It is the value of the coordinate “Y” when X is equal to zero. Here is what it looks like:
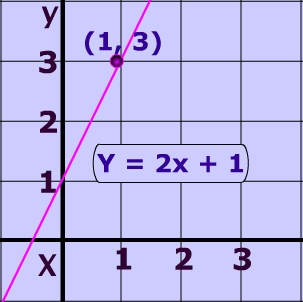
As you can see, the pink-line is hitting the Y-axis (when x is zero) at “1”. That is the y-intercept! Now, the line’s y-coordinate increases by “2” for every increase in “1” of the x-coordinate, that is the slope. Notice they wrote the equation of the line, Y=2X+1, in “slope-intercept form”.
Now let’s look at this graph:
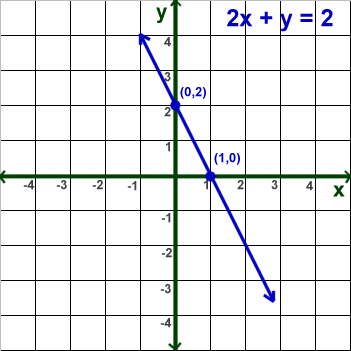
The equation they gave us in NOT in slope-intercept for as the Y variable isn’t by itself on the left side. So let’s move the “2X” over to the right side….
2X + Y = 2 (original equation)
Now, to get Y all by itself, we subtract 2X from both sides (what you do to one side, you have to do to another)….
2X – 2X + Y = 2 – 2X ( now by subtracting 2X from both sides the 2X on the left cancels with the 2X that was there to begin with). The 2Xs on the left cancel…
Y= 2-2X. Let’s move the -2X to be in front of the 2…
Y = -2X + 2.
There, we did it; the equation is now in slope-intercept form. The slope of the line is -2 and the y-intercept is at +2. See the graph also. Notice the blue line intersects the y-axis at 2! And the slope is negative two as from the y-intercept, (0,2), falls two points for every one it goes to the right. The next point is at (1,0).
Homework:
Get the following equations in Slope-intercept form (Y=MX+B) if it isnt’ in that form. State the slope and y-intercept.
- Y = 4X – 3.
- Y = 2/3X +6.
- Y = 9.5 – 3.1X
- 5x + Y = 8
- -6x + Y = 9
Now, write the equation of a line with the following slope and y-intercept:
- Slope, M = 12. Y-intercept is (0,2)
- Y-intercept 7, slope of 4/5
- slope, M = -6, Y-intercept = -6.
Good luck, write down all your steps/work and send them to me!

 Additional settings for Safari Browser.
Additional settings for Safari Browser.







