A good video on finding volume of pyramids.
You have notes on calculating the volume of cones and pyramids so attempt some problems!
1. Find the volume of a cone with a base radius of 4 inches and a height of 10 inches.
2. Find the volume of a cone with a base diameter of 10 inches and a height of 6 inches. You’ll need the radius! How do you get the radius from the diameter???
3. Find the volume of a cube with a side lenght of 5 inches?
4. Find the volume of a rectangular solid with a base area of 20 inches and a height of 8 inches.
5. A rectangular solid has dimensions of length = 8 inches, a width of 4 inches and a height of 10 inches. What is it’s volume?
Good luck! Email me the answers to me via my email at the schoo!
April 16th to April 23rd
Answers to last week’s questions:
#1. Okay, Volume = 1/3*Pi*R^2*H. I used 3.14 for Pi and got a volume of 167.46 cubic inches.
#2. The trick to this one is you need to find the radius from the given diameter. If the diameter is 10 inches the radius is 5 inches! Answer: 157 cubic inches!
#3. Volume of a cube = Side ^ 3! So if the side is 5 inches you just cube it (mulitply it by itself 3 times)...V = 125 inches cubed!
#4. Volume of a rectangular solid is V= Base area * Height. So in this case it is 20 inches (squared) times 8 inches= 160 cubic inches.
#5. Another version of the Volume of a rectangular solid is V=Length * width * height. So we just multiply the three numbers given…. V=4*8*10 = 320 inches cubed.
Simple, eh?
New stuff!
Optimization.
What does that mean? Well, basically it means making something as large as possible while keeping something else as small as possible. You do this all the time. When you go our with your parents to the store to buy food you want to get the most food for the least amount of money spent! You have been “optimizing” your spending money for goods and never knew you were engaging in “optimizing” from a mathematics perspective.
So let’s take a common problem ranchers and farmers in New Mexico have to deal with when they make a corral for animals or a garden. They have a limited amount of money to build the corral (or garden), but they want to maximize the area they are enclosing to either have the most space for their cattle or area to grow plants.
So lets take rancher Erenesto Gutierrez. He can afford 100 feet of fencing for his prized bull “Torro”. So the perimeter of the fence will be 100 feet around and he must create a corral in the shape of a rectangle (say it is a governmen regulation that all corrals must be made in that shape). What shold the dimensions be that produce the largest area for “Torro”? Let’s make a table of the width, length, perimeter and area for this corral: remember, the perimeter equation is P=2*w + 2*h and area is A=L*W.
Width Length Perimeter Area (square feet)
1 49 100 49
2 48 100 96
3 47 100 141
Now, your homework is to continue this table for Torro and tell Ernesto what dimensions he should make his corral so Torro has plenty of room (area in square feet) to run around and eat gamma grass! Take a picture of the entire table with your analysis.
Note: We do this as we know the more room a horse or cow has the “happier” the animal will be thus producing more offspring, more milk, etc. This is very important in the raising of animals or growing a garden and it is a scientific approach to exactly how to use one’s money to maximize the area of the corral (or garden) while spending the least amount of money on fencing.
Also note, I’m only interested in integer values (1, 2, 3, 4, etc.,). In more complicated figures such as trapezoids with some strange perimeters we need calculus to determine the optimum dimensions, but at least now you’ll have a good understanding of what we are looking for in this problem.
So complete the table, take a photograph of it and email it to me! Next week we’ll look at similar problems that you may use in the future.
For further inspiration view this video:
https://www.khanacademy.org/math/pre-algebra/pre-algebra-measurement/prealgebra-perimeter/v/length-and-width-from-perimeter-and-area
April 27th to May 1st
Okay, a quick note on last week’s assignment to maximize the area of “Torro”’s enclosure. To save us some time let’s start with the width at 20 and the Length of 30, increasing the width by one and decreasing the length by 1...
Width Length Perimeter Area
20 30 100 600
21 29 100 609
22 28 100 616
23 27 100 621
24 26 100 624
25 25 100 625
26 24 100 624
27 23 100 621
…………….
I can stop there. When the length and width are EQUAL in a 4 sided figure you maximize the area! 25 times 25 will give you a perimeter of 100, the amount of fencing the farmer could afford, he’ll get the maximum area!
New stuff………..LOGIC!!!
Guess what? You use logic all the time to enhance the quality of almost every decision you make, dialy.
Here is a definition of logic:
“
noun
-
1.
reasoning conducted or assessed according to strict principles of validity. “
So what are these “principles of validity”? Here we go!
Conditional statement: “If P, then Q”? The “P” is everything after the “If” and before the “Then”. It is also known as the “hypothesis”. Q is everything that comes after the “Then”. It is known as the “conclusion”. Example:
“If my name is Bowden Russell, then I am the middle school math teacher at Magdalena Middle School”
P: My name is Bowden Russell (the hypothesis).
Q: I am the math teacher at Magdalean middle school.
(Note, this is a true statement. This will be important)
Converse: If Q, then P!
Yep, if you switch the conclusion with the hypothesis you have the Converse. Example predicated on above:
If I’m the Middle School Math teacher in Magdalena Middle School, then my name is Bowden Russell.
Inverse Statement: Not P then Not Q! More commonly written as:
∼p→∼q.
Example, from our original If P then Q…
If I am NOT the middle school math teacher at Magdalena Middle school the I am not Bowden Russell.
Pretty cool, right?
Now comes my favorite part; The Contrapositive!! This is great. We take the original statement, If P then Q, then find the inverse of the converse!!! Told you it was great!
Not Q then Not P, or usually written: as such:
∼q→∼p
(the little squiggly lines in front of the P and Q mean,”not”).
But here is what I like: If a statement is true, If P then Q and the Contrapositive is true: If not Q then not P, then you have a definition!
Example of a definition:
If a figure has 4 sides, then it is a quadrilateral. Nice, conditional statement with P=”a figure with 4 sides” and Q=”It is a quadrilateral”.
Let’s take the contrapositive of that…
If a figure is NOT a quadrilateral then it doesn’t have 4 sides”.
Hey, that is also a true statement! If a statement is true and it’s contrapositive is also true you have a definition. Of course that is the definition of a 4 sided figure being a quadrilateral!!!!
Definition are important of carry out laws and writing them! For example, courts and judges use these definitions to determine if someone is guilty or innocent of a crime. In the state of New Mexico, if you are caught driving and your blood alcohol level is .08 or greater the law says you are guilty of drunk driving.
If someone is arrested and his blood alcohol level is .07 he doesn’t meet the definition of driving while drunk, thus the judge would have to find the defendant not guilty.
Okay, problems;
1.
Given the statement: If I’am tired then I want to go to sleep.
Write the converse, inverse and contrapositive of the above statement. Is this a definition?
2. If a figure has 3 sides then it is a triangle
Again, find the converse, inverse and contrapositive. Is this a definition?
3. Another, more complicated one: If I am NOT Lowden then I am Bowden.
Write the converse, inverse and contrapositive. Remember, a negative times a negative is a positive!
4. Law of direct reasoning: If P implies Q and Q implies R than P implies R!!!
example: If I am Ruth then I like drawing. If I like drawing I like pencils. So, I can conclude If I am Ruth than I like pencils! This is good stuff and is also used in law enforcement, computer programming and tons of other stuff. Here is yours….
If I am over 18 then I can vote.
Billy is over 18.
What can we conclude about Billy?
Or more complicated:
If I am a citizen of New Mexico the I have to pay New Mexico taxes.
If I pay New Mexico taxes I can vote in New Mexico elections.
So from the two above statements what can I conclude?
Good video to watch:
https://www.mathplanet.com/education/geometry/proof/if-then-statement
Week of May 4th to May 7th
Translations/Reflections
We use Translations and Reflections in computer programming and art as well as Architecture.
Let’s look at Translations first:
Say we have a standard x-y coordinate plane with a triangle located on it:
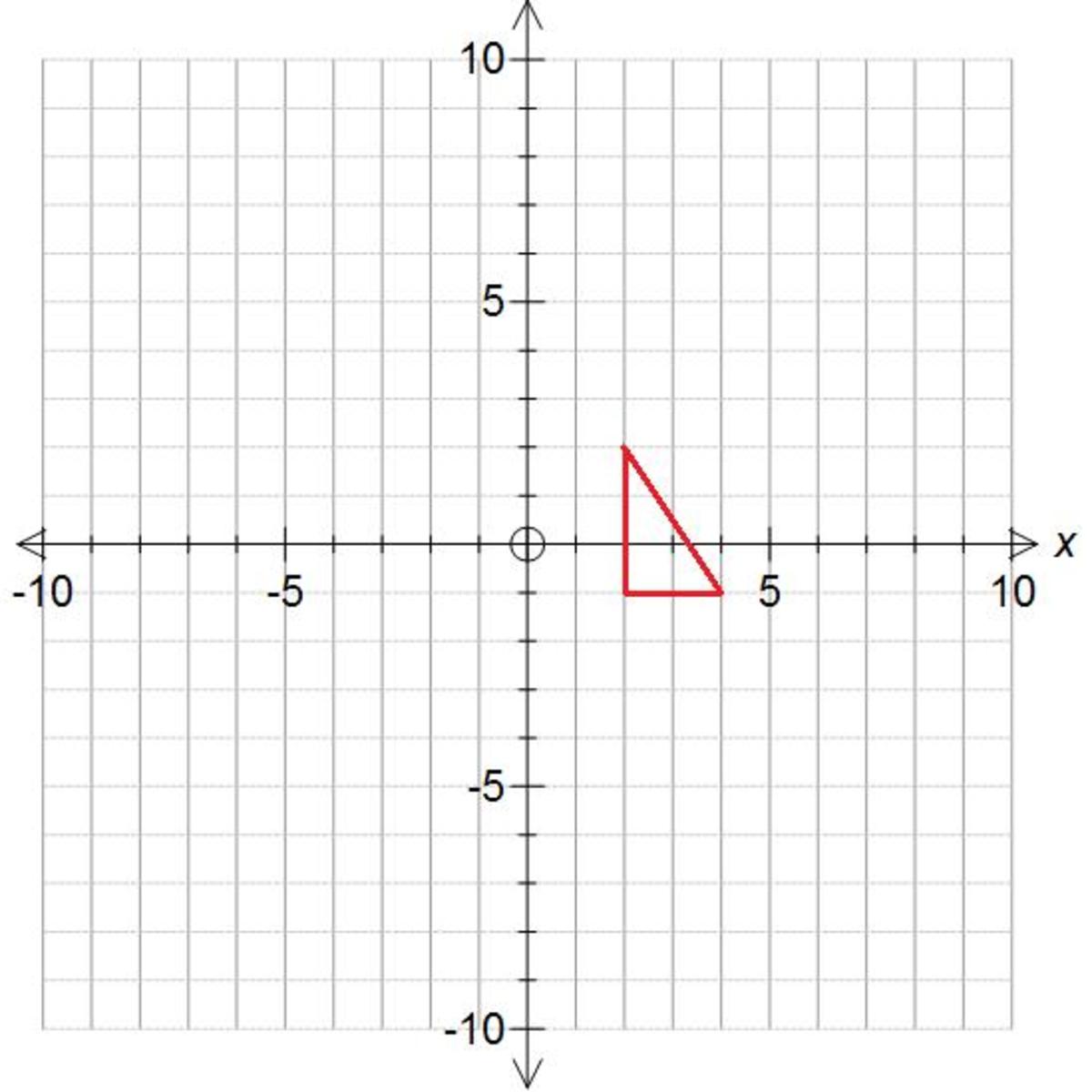
It is a triangle. One point, vertex, is at A(2,-1), another at B(2,2) and the final, right-most point at C(4,-1). If I want to translate the trinagle 4 places to the right I would add 4 to each x-coordinate. Now the three points become A’(6,-1), B’(6,2) and C’(8,-1). Notice the ‘, which in math we call “prime” means the “new” point that the previous point became.
Look at this next example of a trinagle that is being translated:
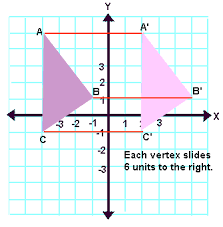
Every vertex, ABC, was tranlated 6 points to the right to form the new, translated trinagle A’B’C’.
Now let’s look at the notation for “translations”. We use “T”.
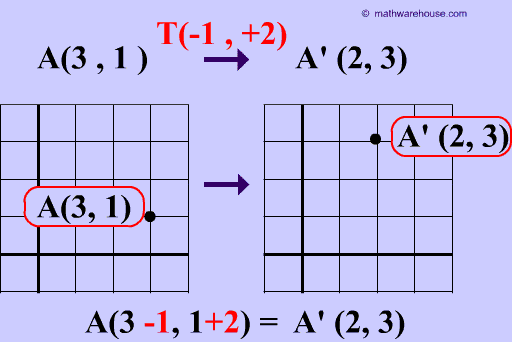
T(-1,+2) means take the original figure, which is point A located at A(3,1) and translate it 1 point to the left (a -1 means move left one) then translate it up 2 points (+2) So notice that point A, at (3,1) to A’ at (2,3).
Let’s work backwards now. Look at the original figure and the translated figure. How many points right did we move the figure and how many points down did I move it?
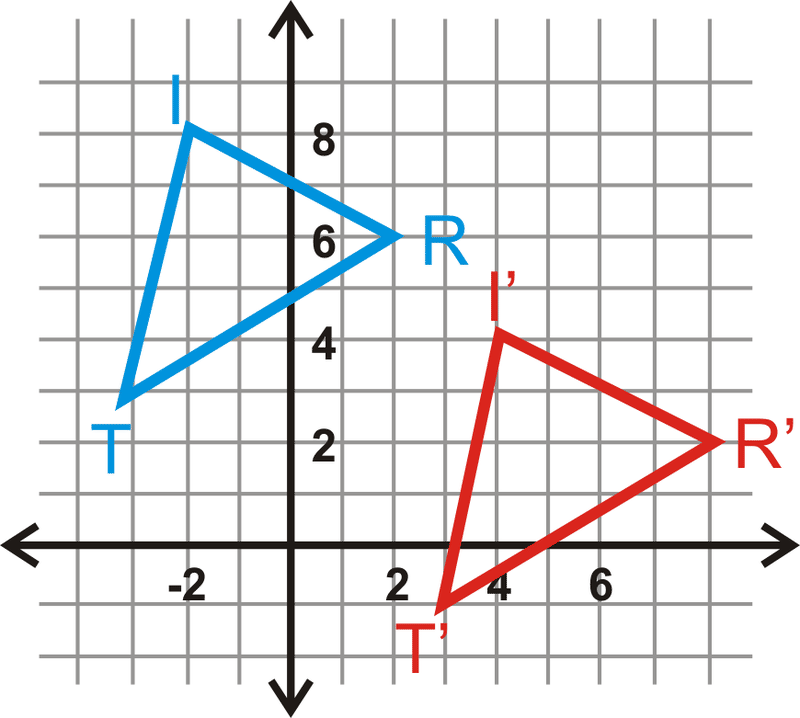
Look at point at “I”. How are did it move to become point “i-prime”? T( ?, ?).
REFLECTIONS:
The figure keeps it’s size, but it’s orientation changes in a reflection. Here is an example:
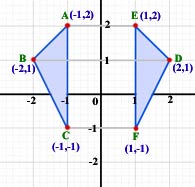
Figure ABC was reflected over the Y-axis to become figure EDF. Notice that point C is the same distance, 1, from the Y-axis as point F. Ditto with point B and D both being two away from the Y-axis.
Rules: When you reflect a figure over the Y-axis just change the sign of the X-coordinate. You don’t even have to graph the figure, but it can help your understnding and visualization of what is happening.
Example: Reflect the points A(1,4), B(-2,3) and C(7,-8) over the Y-axis.
Okay, A becomes A’ by changing the sign on the x-coordinate: A’(-1,4). B’ is now (2,3) and C’ is (-7,8). Easy, eh?
When you reflect a figure over the x-axis just change the sign of the y-coordinate!
Example: Take the line segment with endpoints X(1,8) and Y(8,-2) and reflect it over the x-axis. Answer: X’(1,-8) and Y’(8,2).
Problems to be done and turned in to me
1. Given the following figure with the blue figure being the original figure, what translation did it undergo to become the red figure? T(?,?)

- What if the red figure was the original and the blue was the translated figure? What would the translation look like? T(?,?)
3. Given line segment MN with endpoints M(0,9) and N(9,-8), what are the coordinates of M’N’ if the segment is translated left 6 points?
4. Take trinagle ABC in the following figure and translate it 4 to the right and 2 up, which we say is T(+4,+2). What are the coordinates of A’B’C”?

- What is the translation that took ABC to A’B’C’ in the diagram below:

- Given figure XYZ with coordinate points X(-2,6), Y(0,4) and Z(4,-4) find the coordinates of the figure reflected over the x-axis.
- Now take the same figure in #6, XYZ and relfect it over the y-axis. What are the new coordinates of X’Y’Z’?
8. Okay, take the same figure in #6 and do two reflections! One over the x-axis and one over the y-axis! What are the new coordinates of X’Y’Z’??
9. Now take your answer from #8 and subject X’Y’Z’ to a T(+2,-10). What are the new coordinates of X”Y”Z”?
Good luck!!! Have a great week and get these problems back to me!
8th Grade Week of May 11th to May 15th: DENSITY
Denisty is a really neat subject to study. A simple definition of DENSITY is ‘How much matter (stuff) is packed into how much space (volume).
The formula for Density is :
D = M/V = Mass divided by Volume equals density.
Simple division: just make sure you use the right units.
Mass is usually in Kilgrams or grams. if in Kilograms the volume is usually cubic meters. If in grams the volume is usually in militeres or cubic centimeters (1 ml = 1 cubic centimeter).
So the units of Denisty are either Kilograms/Cubic meter or grams/cubic centimeter, or grams/mililiter.
So let’s wrap our heads around this concept. Denisty is determined by two factors; the mass of an object and how much space (volume) the object takes up. If we take my wedding right, maybe it weighs a couple of ounces-not much-and drop it into Santa Monica bay from the end of the SM pier, my ring, which doesn’t weight that much, sinks to the bottom of the ocean! It’s mass is very, very small, but so is it’s volume.
Now the denisty of ocean water is about 1.027 g/cm^3 (pure water is 1.000 g/cm^3...the salt increases the density). If my ring sinks in the SM bay it must be that it is more dense then the water (it is mostly Gold and the denisty of Gold is 19.3 g/cm^3 so the ring is way, way, way more dense than the ocean water).
When I lived in L.A., I liked to check out the US Naval Ship USS Iowa. It is a HUGE ship; a battleship actually, that was made in 1943. It weights 58,400 tons when fully loaded (each ton is 2000 pounds!!!!). You can visit it for tours as it is now a floating museum:

So why is it my wedding ring sank like a rock and it weights so little, but the USS Iowa weighs so much, but doesn’t sink????
The volume of the USS Iowa was even larger than the mass of the ship! So the density of the IOWA was less than that of the ocean water, thus the IOWA floats on the water. There is lots and lots of empty space in the IOWA thus allowing the volume calculation to be enormous, thus decreasing the density.
As you may know, on April 13th, 1912, the HMS Titanic sank when it hit an iceberg in the North Atlantic. Watch this scene where the ship’s engineer explains to the Ship’s Captain that nothing they could do would stop the ship from sinking. He was able to calculate that when the 5 holds were ripped open by the iceberg, when those holds were filled with water, instead of very light air, the ship was doomed (the entering sea water would dramatically increase the numerator of the ship’s mass without increasing the volume (the space of the holds), thus the density of the ship would be over 1.027 g/cm^3 (a lot more), causing the ship to sink:
https://www.youtube.com/watch?v=SP7BWb1ndpA
They did have pumps that could put some water out, but as the engineer states, the rate at which the pumps could remove the water was much, much less than the rate at which the water was flooding into the ship.
A submarine, though, through use of it’s ballast tanks and compressed air located in the submarine, can manipulate it’s density so it can dive, or surface, when ever it wants. See the diagram and pay attention to the ballast tanks (which can fill with water or air) and the compressed air tanks:

When they want the submarine to dive they allow the air to leave the ballast tanks and allow the sea water to take the place of the air (so the densitry of the sub is now much greater than 1.027 g/cm^3). Submarine will submerge!! See the diagram below:
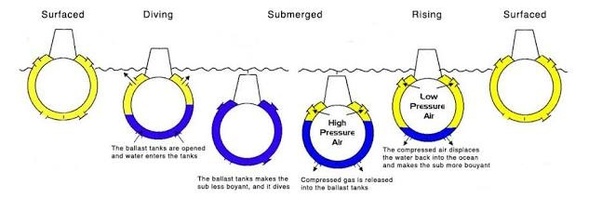
when they want to make the submarine surface they inject high-pressure compressed air into the ballast tank, forcing the water out thus causing the submarine to have a denisty less than the surrounding water, causing it to surface!
See this picture of the USS Archer-Fish? See all the “holes” along the side? Those are the vents that allow water to enter or air to escape. You can’t see it in this picture, but there are also vents on the bottom of the ballast tank that allow water to enter, or leave:

By the way, as a New Mexican you must know this is how a hot-air balloon is able to fly: The hot air that fills the large ballons is much less “dense” than the surrounding out-side cold air (ballons fly best in the cold of morning or evening, not in warm weather).
Once the balloon is filled with hot air it is less dense than the surrounding cold air, thus, like the USS IOWA the ballon will float upwards!!!
 If the pilot wants to go higher, he increases the amount of heated (by a propane heater) air into the ballon. This lessens the densitry so the ballon goes up. If he wants to go down he’ll open the vents at the top allowing the hot air to escape, thus increasing his denstiy, causing the ballons to go down!
If the pilot wants to go higher, he increases the amount of heated (by a propane heater) air into the ballon. This lessens the densitry so the ballon goes up. If he wants to go down he’ll open the vents at the top allowing the hot air to escape, thus increasing his denstiy, causing the ballons to go down!
Problems:
Remember, pay attention to the units and all you do is divide. Next week we will do some more complicated Density problems.
1. A man builds a boat that has a volume of 808 cubic meters. If the boat weighs 805 Kilograms what is the denisty of this boat? Will it float in the ocean? If so, why?
2. Gold has a densitry of some 19.3 grams/cubic centimeter. Your best friend says he has a piece of gold and wants to sell it to you for a great deal of $1,000!! You decide to see if it has the same denisty of Gold! It weights 6.45 grams and when you put it in the glass of water the water level rises .744 cubic centimeters. (This is how you tell the volume of an irregular object; fully submerge it in water and the level the water rises is it’s volume! It’s called Archamedes’ Principle). Do the division to see how close the object’s denisty is to Gold! Is it close to Gold?
3. Joe Stephanski had a small box that he thinks is made of silver He measures the length to be 3.6 cm, the width to be 2.5 cm and the height to be 4.0 cm. The object has a mass of 37.7 Kilograms (37700 grams). Do the division (after you calculate the volume of the box of course) and compare it to the accepted value of silver. Use Google to find the denisty of silver.
4. Jessie James has a small sphere he thinks is made of copper. The radius of the sphere is 1.4 centimeters. It weighs 22 grams. Does it have the denistry of copper? Again, calculate the volume then do the division. Look up the density of copper and compare. Do you remember the equation for the volume of a sphere? It can be found on Google should you forget.
5. A ballon filled with helium has a volume of .5 cubic meters. If the weight of the helium gas in the ballon is .0004 kilograms, what is its denisty? Compare this to the denisty of at about 65 degrees F which is around 1.2 Kg/cubic meter. Does this explain why helium ballons float in the air? Look up the density of air to compare. Watch your units.
Make sure you explain your answer using complete sentences and showing your work!

 Additional settings for Safari Browser.
Additional settings for Safari Browser.











